Trong tài chính, NPV (Net Present Value – Giá trị hiện tại thuần) của các dòng tiền nhận được vào các thời điểm khác nhau trong tương lai là giá trị của các dòng tiền đó tại thời điểm hiện tại.
NPV thường được dùng để đánh giá hiệu quả của dự án, 1 dự án có NPV ≥ 0 có nghĩa là khả thi và mang lại lợi nhuận cho công ty; ngược lại, NPV < 0 là dự án không khả thi và khiến công ty bị lỗ. Bài dưới đây sẽ hướng dẫn cách đánh giá hiệu quả dự án sử dụng 3 hàm Excel là PV, NPV và XNPV (file mẫu sử dụng trong bài được đính kèm ở dưới)
1. Trường hợp luồng tiền đều qua các kỳ cách đều nhau – hàm PV
a. Công thức: PV(rate, nper, pmt, [fv], [type])
– rate: lãi suất
– nper – number of period: số kỳ nhận được dòng tiền.
– pmt – payment amount: số tiền nhận được từng kỳ.
– fv – optional: giá trị tương lai
– Type (0/1) – optional: mặc định là 0 khi thanh toán vào cuối kỳ và là 1 khi thanh toán đầu kỳ.
b. Ví dụ 1 : công ty A đang xem xét việc đầu tư vào 1 thiết bị sản xuất dự kiến sẽ đem lại nguồn tiền đều 25000$ trong vòng 10 năm tới, lãi suất chiết khấu kỳ vọng là 15%. Câu hỏi là nếu giá của của thiết bị đó là 120000$ thì công ty A có nên mua hay không?
Tại ô C7 ta nhập công thức: =PV(C4,C5,C3) (trường hợp này không cần nhập Fv) sẽ ra kết quả là -125.469, vì hàm PV thể hiện số tiền phải trả hiện tại (cash outflow) để nhận được các dòng tiền trong tương lai nên sẽ hiển thị dấu âm, để lấy giá trị hiện tại của dòng tiền (inflow) ta thêm dấu âm vào trước công thức để có kết quả là 125.469.
Tại ô C8, nhập công thức =C6 + C7 để có được NPV, ở đây NPV = 5469$ > 0 –> dự án khả thi
2. Trường hợp luồng tiền không đều qua các kỳ cách đều nhau- hàm NPV
a. Công thức: NPV(rate, value1, value2,…)
– rate: lãi suất
– value1, value2…: dòng tiền qua các năm (tối đa 254 giá trị với Excel 2007 trở lên, 29 giá trị với Excel 2003 trở về trước) và phải xuất hiện ở cuối mỗi kỳ
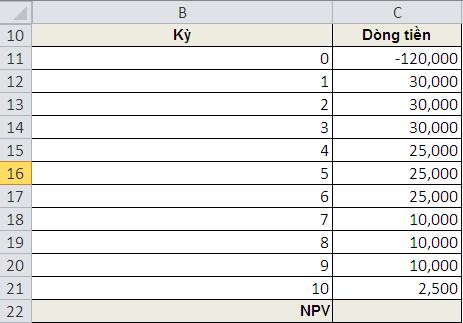
b. Ví dụ 2: vẫn lấy ví dụ ở trên, tuy nhiên dòng tiền nhận được từ năm 1-10 sẽ không đều (như hình dưới), trường hợp này chúng ta không sử dụng được hàm PV
Mọi chuyện lại rất đơn giản khi sử dụng hàm NPV, tại ô C22 nhập =NPV(0.15,C12:C21)+C11 = -3483$ <0 –> dự án không khả thi
(kỳ 0 thể hiện số tiền phải chi trả để mua thiết bị)
3. Trường hợp luồng tiền xuất hiện tại kỳ không đều nhau- hàm XNPV
a. Công thức: XNPV(rate, values, dates)
– rate: lãi suất
– Values: (bắt buộc) dòng tiền nhận được qua các kỳ tương ứng
– dates: (bắt buộc) lịch biểu gồm các ngày chi trả tương ứng với các khoản chi trả của dòng tiền
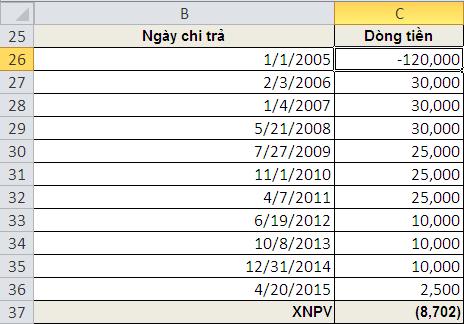
b. Ví dụ 3: vẫn các ví dụ ở trên nhưng lần này dòng tiền chi trả taị các kỳ không đều nhau (như hình dưới), trong đó 1/1/2005 là ngày chi trả tiền mua thiết bị, trường hợp này rất khó để sử dụng hàm NPV và PV.
Giải quyết bằng cách dùng hàm XNPV, tại ô C37 nhập công thức =XNPV(0.15,C26:C36,B26:B36), kết quả là -8072$ –> dự án không khả thi.
Ngoài NPV, một phương pháp nữa thường được sử dụng khi đánh giá dự án là IRR (tỷ suất hoàn vốn nội bộ), bài viết sau sẽ đề cập đến vấn đề này.

Comments ( 3 )